Recursive Generation Algorithm
(This post continues from the previous post. Read it first.)
Using the method proposed here by Eli Bendersky, I have developed an algorithm to stop infinite recursion when expanding a recursively-defined nonterminal symbol.
Each time a specific nonterminal is expanded, the future probability of expanding that nonterminal in the same way is decreased. However, the probability decrease is only observed by lower levels of recursion, preventing typically early nonterminal symbols from altering the probabilities of typically later nonterminal symbols systematically.
The Algorithm
Terms
- Recursive Production: a production that is defined in terms of itself. The symbol itself is part of a possible expansion.
- Lexical Production: a production which defines a nonterminal symbol with all terminal symbols. The definition is typically recognizable as words in a natural language.
CFG
'S': [
('S', 'NP'), # recursive
('S', 'S', 'VP'), # recursive
('NP', 'VP'), # non-recursive
],
'NP': [
('NN',), # non-recursive
('ADJ', 'NP'), # recursive
('blue', 'NP'), # recursive
('green', 'NP'), # recursive
],
'VP': [('V',)], # non-recursive
'NN': [('I',)], # lexical production
'V': [('am',)] # lexical production
Code
import copy
import random
def expand(symbol, rules, alpha=0.25):
"""
Initialize a dict which will contain weights for each production used at
each level of recursion. rule_weights is passed by shallow copy between
levels of recursion to avoid mutating an upper level's weights.
Args:
symbol (str): The symbol from which to begin expansion. Must be
contained in rules
rules (dict): Nonterminal symbols and their expansion possibilities
key: str
value: list of tuples
ex. rules = {
'S': [('S', 'NP'), # Possible expansions
('S', 'S', 'VP'), # ...
('NP', 'VP')], # ...
'NP': [...],
...}
alpha (float): Penalization parameter for repeated expansions. Alpha
is multiplied by the previous probability of a chosen expansion, so
probability of repeated expansion decreases as value decreases.
P = alpha ** N
where P is probability of expansion being chosen
N is number of times the rule has been expanded in the
current depth-first traversal.
0 < alpha < 1.0
Returns:
tuple of str: A grammatical sentence according to CFG
"""
# Initialize dict values to 1.0
rule_weights = {}
def recurse(symbol, rule_weights):
sentence = ()
# Initialize nonterminal expansion weights
if symbol not in rule_weights:
rule_weights[symbol] = [1.0,] * len(rules[symbol])
# else, they're already set in an upper recursion level
random_expansion = random.choices(population=rules[symbol],
weights=rule_weights[symbol],
k=1)[0] # NOTE
# Assumes len(list) == 1
# Decrease future probability of chosen rule
# NOTE Assumes only one match of random_expansion in rules[symbol]
rule_weights[symbol][rules[symbol].index(random_expansion)] *= alpha
for rhs_symbol in random_expansion:
if rhs_symbol in rules: # nonterminal symbol
sentence += recurse(rhs_symbol, copy.copy(rule_weights))
else: # terminal symbol
sentence += (rhs_symbol,)
return sentence
return recurse(symbol, rule_weights)
Output
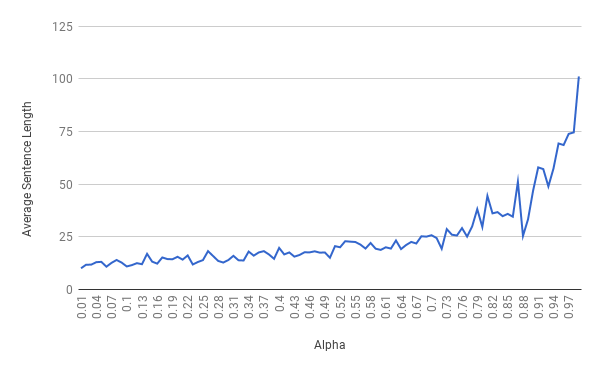
To learn a little about the behavior of alpha in the algorithm, I found the average sentence length over 100 runs of expand() for each alpha from 0.01 - 0.99 with a step of 0.01.
This is the output when using the sample CFG above. It appears that we have an exponential curve as alpha approaches 1. This is reasonable, since P = alpha^N where N = number of times a rule has been chosen in the current traversal.
The same analysis can be seen for the algorithm by Eli Bendersky, on which mine is based.
Discussion
- The
recurse()function inside the outerexpand()function relieves the user of creating therule_weightsdict themselves, while still allowing it to be passed as a parameter to the recursive function - The
rule_weightsdict is a mutable type, however, so it is copied before passing down the stack to avoid mutating its state in upper levels of the stack. - I’ve made
# NOTEs of assumptions the code makes, but they are valid if the envisioned use doesn’t change. Which it will. - That means these
# NOTEs will have to be revisited.
Comments and suggestions welcome!